Métodos de suavizado#
Suavizado Exponencial Simple (SES):#
El Suavizado Exponencial Simple (SES) es un método de pronóstico univariante para series de tiempo que combina el valor más reciente de la serie con el nivel suavizado anterior, asignando un peso decreciente a medida que los datos son más antiguos.
Se utiliza principalmente cuando la serie no presenta tendencia ni estacionalidad marcada, o cuando buscamos un pronóstico muy “reactivo” a los cambios recientes.
Fórmula recursiva y componentes:#
Denotemos por:
\(y_t\): valor observado de la serie en el período \(t\).
\(S_t\): nivel suavizado en el período \(t\).
\(\alpha\): parámetro de suavizado, con \(0 < \alpha < 1\).
La ecuación recursiva del SES es:
Término de actualización \(\alpha\,y_t\): incorpora el valor actual con peso \(\alpha\).
Término de persistencia \((1-\alpha)\,S_{t-1}\): conserva el nivel suavizado anterior con peso \((1-\alpha)\).
Interpretación del parámetro \(\alpha\)#
\(\alpha\) cercano a 1:
Suavizado «ligero», el pronóstico responde rápidamente a cambios recientes.
Mayor varianza en la serie suavizada.
\(\alpha\) cercano a 0:
Suavizado «fuerte», la serie suavizada es muy estable y reacciona lentamente.
Menor varianza, pero tarda en reflejar cambios recientes.
En la práctica, \(\alpha\) se elige minimizando un criterio de error (por ejemplo, MSE) sobre los datos históricos, o bien probando varios valores y seleccionando el que ofrezca el mejor balance entre reaccionar a cambios y reducir ruido.
Pronóstico con SES:#
Una gran ventaja de SES es que el pronóstico a uno o más pasos se obtiene directamente del último nivel suavizado:
Es decir, todos los pronósticos futuros son iguales al nivel suavizado más reciente.
Ventajas y limitaciones:#
Ventajas
Muy sencillo de implementar y comprender.
Pocos parámetros (\(\alpha\)).
Requiere escaso almacenamiento (solo \(S_{t-1}\)).
Óptimo para series sin tendencia ni estacionalidad.
Limitaciones
No capta tendencia ni patrones estacionales.
Pronósticos convergen a un nivel constante.
Sensible a la elección de \(\alpha\).
Pasos prácticos de implementación:#
Inicialización
Tomar \(S_1 = y_1\).
Alternativamente, usar la media de los primeros \(k\) valores para \(S_k\).
Recursión
Para cada \(t = 2, 3, \dots, T\), actualizar \(S_t\) con la fórmula recursiva.
Cálculo del pronóstico
Para cada \(h \ge 1\), fijar \(\hat{y}_{T+h} = S_T\).
Selección de :math:`alpha`
Fit manual: probar varios valores (por ejemplo, de 0.1 en 0.1) y calcular MSE.
Fit automático: optimizar \(\alpha\) mediante minimización de MSE.
Ejemplo:#
Supongamos la serie \(\{y_t\} = [10,\;12,\;11,\;13,\;12]\) y \(\alpha = 0.5\):
\(S_1 = 10\)
\(S_2 = 0.5\cdot12 + 0.5\cdot10 = 11\)
\(S_3 = 0.5\cdot11 + 0.5\cdot11 = 11\)
\(S_4 = 0.5\cdot13 + 0.5\cdot11 = 12\)
\(S_5 = 0.5\cdot12 + 0.5\cdot12 = 12\)
El pronóstico a cualquier paso futuro será \(\hat{y}_{6} = 12\).
Conexión con otros métodos:#
Holt (doble suavizado): agrega un componente de tendencia.
Holt–Winters: extiende SES a datos con estacionalidad.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Generar serie de tiempo sin tendencia ni estacionalidad (solo ruido alrededor de un nivel)
np.random.seed(123)
periods = 100
dates = pd.date_range(start='2021-01-01', periods=periods, freq='D')
level = 10
noise = np.random.normal(loc=0, scale=1.0, size=periods)
series = pd.Series(level + noise, index=dates)
# Función SES recursiva
def ses(series, alpha):
result = [series.iloc[0]]
for t in range(1, len(series)):
result.append(alpha * series.iloc[t] + (1 - alpha) * result[-1])
return pd.Series(result, index=series.index)
# Aplicar SES para distintos alpha
alphas = [0.2, 0.5, 0.8]
smoothed = {alpha: ses(series, alpha) for alpha in alphas}
# Graficar resultados
plt.figure(figsize=(10, 5))
plt.plot(series, label='Serie original', color='black', linewidth=1.5)
for alpha, smooth in smoothed.items():
plt.plot(smooth, label=f'α = {alpha}', alpha=0.6)
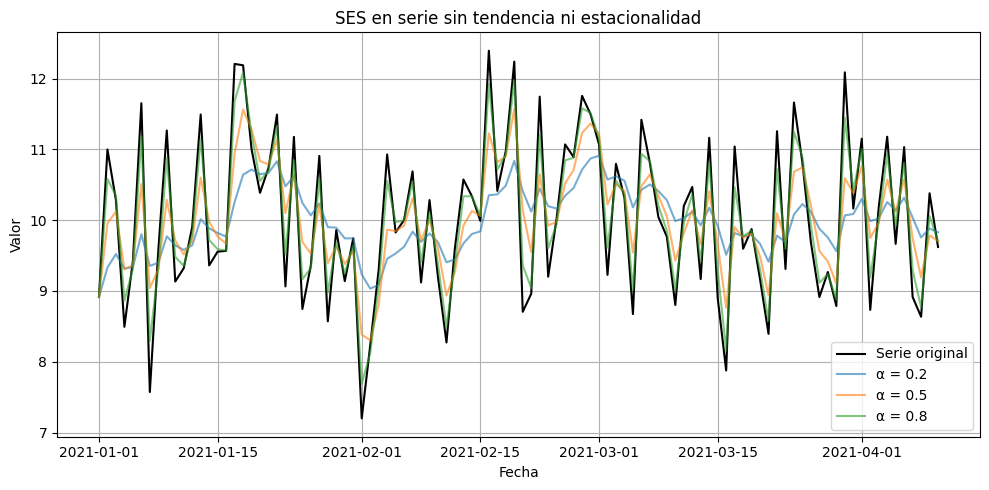
plt.title('SES en serie sin tendencia ni estacionalidad')
plt.xlabel('Fecha')
plt.ylabel('Valor')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
SimpleExpSmoothing (SES) — statsmodels#
La clase SimpleExpSmoothing del módulo
statsmodels.tsa.holtwinters implementa el método de Suavizado
Exponencial Simple (SES), una técnica de pronóstico para series de
tiempo que no presentan tendencia ni estacionalidad.
Este método suaviza la serie otorgando mayor peso a los valores más recientes, mediante un parámetro de suavizado \(\alpha \in (0, 1)\). A diferencia de otros modelos, SES produce pronósticos constantes iguales al último valor suavizado.
SimpleExpSmoothing(endog, initialization_method=None, initial_level=None)
endog: debe ser un objeto pd.Series con índice temporal.
optimized=True: permite que el modelo escoja el mejor valor de
\(\alpha\) minimizando el error cuadrático medio (MSE) en los datos.
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
# Ajustar SES con alpha optimizado automáticamente
model = SimpleExpSmoothing(series).fit(optimized=True)
fitted_values = model.fittedvalues
alpha_opt = model.model.params['smoothing_level']
# Graficar resultados
plt.figure(figsize=(10, 5))
plt.plot(series, label='Serie original', color='black')
plt.plot(fitted_values, label=f'Suavizado SES (α optimizado = {alpha_opt:.4f})', color='blue')
plt.title('Ajuste con Suavizado Exponencial Simple (SES)')
plt.xlabel('Fecha')
plt.ylabel('Valor')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
optimized=True: permite que el modelo escoja el mejor valor de
\(\alpha\) minimizando el error cuadrático medio (MSE) en los datos.
Ajustar el modelo con un valor específico de alpha (por ejemplo, 0.3):
alpha = 0.3
model = SimpleExpSmoothing(series).fit(smoothing_level=alpha, optimized=False)
# Hacer pronóstico fuera de la muestra
horizon = 10 # número de pasos futuros a predecir
forecast_index = pd.date_range(start=series.index[-1] + pd.Timedelta(days=1), periods=horizon, freq='D')
forecast = model.forecast(horizon)
forecast = pd.Series(forecast.values, index=forecast_index)
# Graficar serie, ajuste y pronóstico
plt.figure(figsize=(10, 5))
plt.plot(series, label='Serie original', color='black')
plt.plot(fitted_values, label=f'Suavizado SES (α optimizado = {alpha_opt:.4f})', color='blue')
plt.plot(forecast, label='Pronóstico', color='red', linestyle='--')
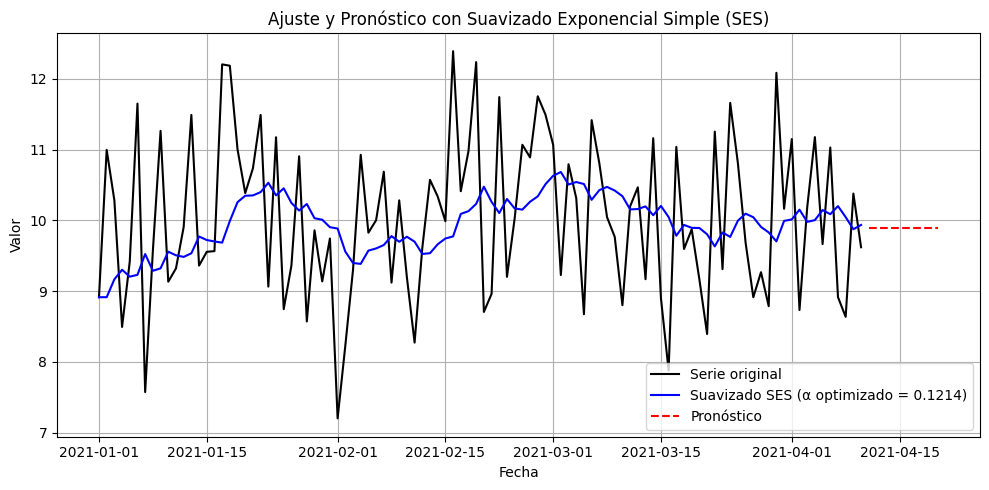
plt.title('Ajuste y Pronóstico con Suavizado Exponencial Simple (SES)')
plt.xlabel('Fecha')
plt.ylabel('Valor')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
¿Qué significa que \(\alpha = 1\) en el Suavizado Exponencial Simple (SES)?
Cuando se aplica el método de Suavizado Exponencial Simple (SES) y el valor óptimo de \(\alpha\) resulta ser igual a 1, esto tiene una interpretación específica y consecuencias importantes en el comportamiento del modelo.
El SES se define mediante la fórmula recursiva:
Donde:
\(y_t\) es el valor observado en el tiempo \(t\)
\(S_t\) es el valor suavizado en el tiempo \(t\)
\(\alpha\) es el parámetro de suavizado, con \(0 < \alpha < 1\)
Si \(\alpha = 1\), la fórmula se simplifica a:
Esto significa que:
El valor suavizado en cada período es igual al valor observado actual.
No hay influencia del pasado: el modelo no retiene memoria.
El modelo no suaviza nada — simplemente replica la serie original sin filtrarla.
Implicaciones prácticas:
No se produce ningún efecto de “suavizado”: se comporta como una copia directa de la serie.
- El pronóstico será simplemente el último valor observado:\[\hat{y}_{t+h} = y_t\]
No hay reducción de ruido ni modelado de dinámica subyacente.
¿Por qué puede suceder esto?
La serie puede ser muy volátil o errática, sin patrones claros que puedan ser capturados por un nivel suavizado.
El modelo, al minimizar el error (ej. MSE), prefiere seguir exactamente los datos en lugar de suavizarlos.
Podría indicar que el SES no es el método adecuado para esa serie.
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
# Descargar datos mensuales desde 2015
start_date = "2020-01-01"
end_date = "2025-07-31"
# TRM de Colombia (USD/COP)
serie = yf.download("ECOPETROL.CL", start=start_date, end=end_date, interval='1mo', auto_adjust=False)['Close']
serie.name = 'Serie de tiempo'
# Establecer frecuencia explícita para evitar el warning de statsmodels
serie.index.freq = serie.index.inferred_freq
# Crear figura
plt.figure(figsize=(10, 5))
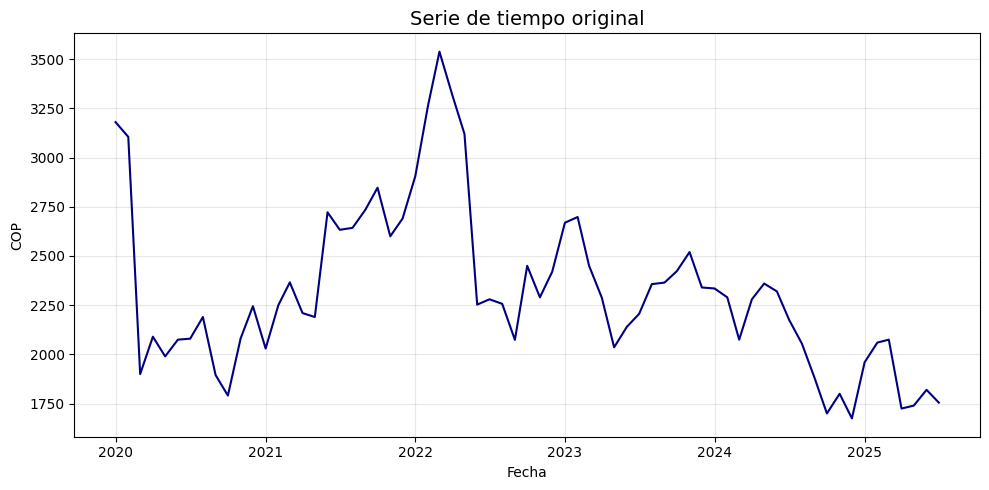
plt.plot(serie.index, serie, linestyle='-', color='navy')
# Personalización del gráfico
plt.title("Serie de tiempo original", fontsize=14)
plt.xlabel("Fecha")
plt.ylabel("COP")
plt.grid(True, alpha=0.3)
# Formato de fechas en el eje X
plt.gca().xaxis.set_major_locator(mdates.YearLocator())
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
plt.tight_layout()
plt.show()
[*******************100%*********************] 1 of 1 completed
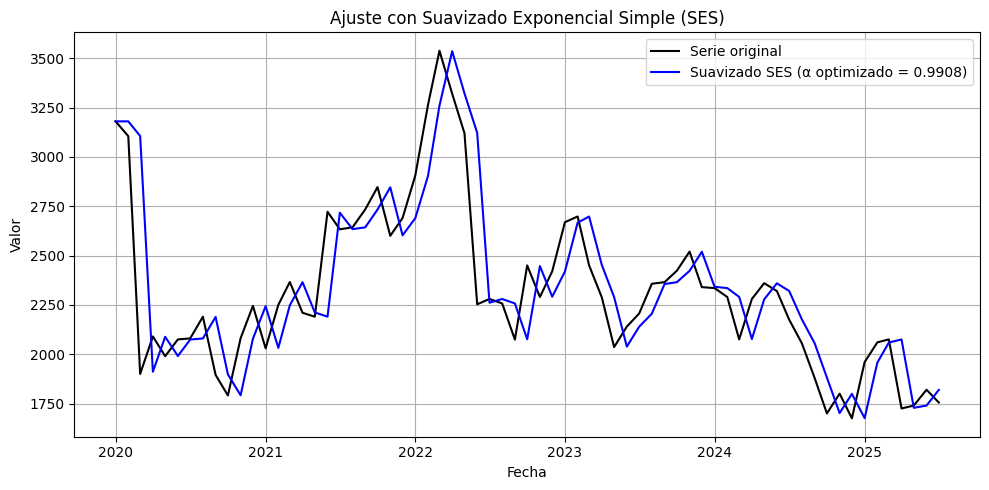
# Ajustar SES con alpha optimizado automáticamente
model = SimpleExpSmoothing(serie).fit(optimized=True)
fitted_values = model.fittedvalues
alpha_opt = model.model.params['smoothing_level']
# Graficar resultados
plt.figure(figsize=(10, 5))
plt.plot(serie, label='Serie original', color='black')
plt.plot(fitted_values, label=f'Suavizado SES (α optimizado = {alpha_opt:.4f})', color='blue')
plt.title('Ajuste con Suavizado Exponencial Simple (SES)')
plt.xlabel('Fecha')
plt.ylabel('Valor')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
Método de Holt (Suavizado Exponencial Doble):#
El método de Holt, también conocido como suavizado exponencial doble, es una extensión del Suavizado Exponencial Simple (SES) que permite modelar series de tiempo con tendencia, pero sin estacionalidad. Introduce un segundo componente llamado tendencia, que evoluciona en el tiempo y se ajusta junto al nivel de la serie.
Componentes del modelo:
El modelo de Holt tiene dos ecuaciones principales:
Nivel \(L_t\): representa el valor suavizado de la serie.
Tendencia \(T_t\): representa el cambio esperado entre períodos.
La formulación del modelo es:
Donde:
\(y_t\): valor observado en el tiempo \(t\)
\(L_t\): nivel estimado en el tiempo \(t\)
\(T_t\): tendencia estimada en el tiempo \(t\)
\(\hat{y}_{t+h}\): pronóstico a \(h\) pasos adelante
\(\alpha \in (0,1)\): parámetro de suavizado para el nivel
\(\beta \in (0,1)\): parámetro de suavizado para la tendencia
Interpretación_
Nivel \(L_t\): suaviza los valores observados, considerando el efecto de la tendencia.
Tendencia \(T_t\): captura el cambio promedio entre períodos y se actualiza dinámicamente.
Pronóstico: se realiza extrapolando el último nivel más \(h\) veces la tendencia estimada.
¿Cuándo usar el modelo de Holt?
Usar cuando:
La serie presenta una tendencia clara y sostenida.
No hay estacionalidad (ni semanal, ni mensual).
Se desea un modelo interpretable con componente de crecimiento o decrecimiento.
Ventajas del método de Holt:
Permite capturar tendencias crecientes o decrecientes de forma explícita.
Es una extensión simple y eficiente del SES.
Funciona bien con datos sin estacionalidad, pero con patrones lineales persistentes.
Limitaciones:
No modela estacionalidad. Para eso, se debe usar Holt-Winters.
Si la tendencia cambia bruscamente, el modelo puede sobrerreaccionar o subestimar.
El modelo puede divergir en el tiempo si la tendencia estimada es inestable.
Ejemplo del método de Holt (suavizado doble):#
Nivel inicial: \(L_1 = y_1 = 10\)
Tendencia inicial: \(T_1 = y_2 - y_1 = 12 - 10 = 2\)
Aplicamos las fórmulas de Holt:
- \(L_2 = 0.4 \cdot 12 + 0.6 \cdot (10 + 2) = 4.8 + 7.2 = 12.0\)\(T_2 = 0.3 \cdot (12.0 - 10.0) + 0.7 \cdot 2.0 = 0.6 + 1.4 = 2.0\)
- \(L_3 = 0.4 \cdot 11 + 0.6 \cdot (12.0 + 2.0) = 4.4 + 8.4 = 12.8\)\(T_3 = 0.3 \cdot (12.8 - 12.0) + 0.7 \cdot 2.0 = 0.24 + 1.4 = 1.64\)
- \(L_4 = 0.4 \cdot 13 + 0.6 \cdot (12.8 + 1.64) = 5.2 + 8.664 = 13.864\)\(T_4 = 0.3 \cdot (13.864 - 12.8) + 0.7 \cdot 1.64 = 0.3192 + 1.148 = 1.4672\)
- \(L_5 = 0.4 \cdot 12 + 0.6 \cdot (13.864 + 1.4672) = 4.8 + 9.3997 = 14.1997\)\(T_5 = 0.3 \cdot (14.1997 - 13.864) + 0.7 \cdot 1.4672 = 0.1007 + 1.027 = 1.1277\)
Pronóstico#
Usamos la fórmula \(\hat{y}_{t+h} = L_t + h \cdot T_t\).
- Pronóstico para \(t = 6\):\(\hat{y}_6 = L_5 + 1 \cdot T_5 = 14.1997 + 1.1277 = 15.3274\)
- Pronóstico para \(t = 7\):\(\hat{y}_7 = L_5 + 2 \cdot T_5 = 14.1997 + 2 \cdot 1.1277 = 16.4551\) —
El método de Holt permite capturar la tendencia de crecimiento o decrecimiento y extrapolarla hacia el futuro de forma más precisa que el SES.
from statsmodels.tsa.holtwinters import Holt
# Ajuste del modelo de Holt (suavizado doble)
model = Holt(serie).fit(optimized=True)
fitted_values = model.fittedvalues
# Extraer parámetros optimizados
alpha_opt = model.model.params['smoothing_level']
beta_opt = model.model.params['smoothing_trend']
# Graficar resultados
plt.figure(figsize=(10, 5))
plt.plot(serie, label='Serie original', color='black')
plt.plot(fitted_values, label=f'Holt: α = {alpha_opt:.4f}, β = {beta_opt:.4f}', color='darkgreen')
plt.title('Ajuste con Suavizado Exponencial Doble (Holt)')
plt.xlabel('Fecha')
plt.ylabel('Valor')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
Método de Holt-Winters (Suavizado Exponencial Triple):#
El método de Holt-Winters, también conocido como suavizado exponencial triple, es una extensión del método de Holt que incorpora estacionalidad. Es ideal para modelar series de tiempo con:
Tendencia (creciente o decreciente)
Estacionalidad (patrón cíclico recurrente)
Nivel base (valor promedio del proceso)
Componentes del modelo:
El modelo tiene tres componentes principales:
Nivel (\(L_t\)): valor suavizado central de la serie.
Tendencia (\(T_t\)): cambio esperado en el nivel entre períodos.
Estacionalidad (\(S_t\)): patrón estacional que se repite cada \(m\) períodos.
Existen dos versiones del modelo: aditiva y multiplicativa, según cómo interactúa la estacionalidad con el nivel.
Versión aditiva (para estacionalidad constante en magnitud):
\(m\): número de períodos por ciclo estacional (ej. 12 para datos mensuales con estacionalidad anual)
\(k = \left\lfloor \frac{h-1}{m} \right\rfloor\): ciclos completos transcurridos
Versión multiplicativa (para estacionalidad proporcional al nivel):
Parámetros:
\(\alpha\): parámetro de suavizado del nivel (\(0 < \alpha < 1\))
\(\beta\): parámetro de suavizado de la tendencia
\(\gamma\): parámetro de suavizado de la estacionalidad
¿Cuándo usar aditivo vs multiplicativo?
Tipo de estacionalidad |
Usar modelo |
Ejemplo |
|---|---|---|
Constante en magnitud |
Aditivo |
Demanda sube 100 unidades cada diciembre |
Proporcional al nivel |
Multiplicativo |
Ventas suben 10% cada diciembre |
Ventajas del método de Holt-Winters:
Capta tendencia y estacionalidad simultáneamente.
Genera pronósticos que reflejan el comportamiento cíclico de la serie.
Es fácil de implementar y optimizar automáticamente.
Limitaciones:
Puede fallar si la estacionalidad no es regular o cambia con el tiempo.
Asume que el patrón estacional se repite exactamente cada \(m\) períodos.
No es ideal para series financieras diarias con alta volatilidad.
Ejemplo del método de Holt-Winters (versión aditiva):
Supongamos una serie con estacionalidad anual mensual (\(m = 3\) para simplificar el ejemplo), con valores:
\(\{y_t\} = [30,\; 40,\; 50,\; 35,\; 45,\; 55]\)
Esta serie tiene estacionalidad de 3 meses (por simplicidad didáctica), y se repiten patrones como:
Mes 1: 30 → 35
Mes 2: 40 → 45
Mes 3: 50 → 55
Usamos los parámetros:
\(\alpha = 0.5\) (nivel)
\(\beta = 0.3\) (tendencia)
\(\gamma = 0.2\) (estacionalidad)
Inicializamos:
\(L_3 = y_3 = 50\)
\(T_3 = \frac{y_3 - y_1}{2} = \frac{50 - 30}{2} = 10\)
Estacionalidad inicial:
\(S_1 = y_1 - L_3 = 30 - 50 = -20\)
\(S_2 = y_2 - L_3 = 40 - 50 = -10\)
\(S_3 = y_3 - L_3 = 50 - 50 = 0\)
Ahora aplicamos el modelo:
Paso 4: \(y_4 = 35\)
\(L_4 = 0.5 \cdot (35 - S_1) + 0.5 \cdot (L_3 + T_3) = 0.5 \cdot (35 + 20) + 0.5 \cdot (50 + 10) = 27.5 + 30 = 57.5\)
\(T_4 = 0.3 \cdot (57.5 - 50) + 0.7 \cdot 10 = 2.25 + 7 = 9.25\)
\(S_4 = 0.2 \cdot (35 - 57.5) + 0.8 \cdot (-20) = -4.5 - 16 = -20.5\)
Paso 5: \(y_5 = 45\)
\(L_5 = 0.5 \cdot (45 - S_2) + 0.5 \cdot (57.5 + 9.25) = 0.5 \cdot (45 + 10) + 0.5 \cdot 66.75 = 27.5 + 33.375 = 60.875\)
\(T_5 = 0.3 \cdot (60.875 - 57.5) + 0.7 \cdot 9.25 = 1.0125 + 6.475 = 7.4875\)
\(S_5 = 0.2 \cdot (45 - 60.875) + 0.8 \cdot (-10) = -3.175 - 8 = -11.175\)
Paso 6: \(y_6 = 55\)
\(L_6 = 0.5 \cdot (55 - S_3) + 0.5 \cdot (60.875 + 7.4875) = 0.5 \cdot 55 + 0.5 \cdot 68.3625 = 27.5 + 34.18125 = 61.68125\)
\(T_6 = 0.3 \cdot (61.68125 - 60.875) + 0.7 \cdot 7.4875 = 0.241875 + 5.24125 = 5.483125\)
\(S_6 = 0.2 \cdot (55 - 61.68125) + 0.8 \cdot 0 = -1.33625 + 0 = -1.33625\)
Pronóstico:
Usamos:
Para \(t = 6\), queremos predecir \(t = 7\), \(t = 8\) y \(t = 9\):
\(\hat{y}_7 = L_6 + 1 \cdot T_6 + S_4 = 61.68125 + 5.483125 + (-20.5) = 46.6644\)
\(\hat{y}_8 = L_6 + 2 \cdot T_6 + S_5 = 61.68125 + 10.96625 + (-11.175) = 61.4725\)
\(\hat{y}_9 = L_6 + 3 \cdot T_6 + S_6 = 61.68125 + 16.449375 + (-1.33625) = 76.7944\) Este ejemplo muestra cómo Holt-Winters descompone una serie en nivel, tendencia y estacionalidad para generar pronósticos coherentes con su comportamiento cíclico.
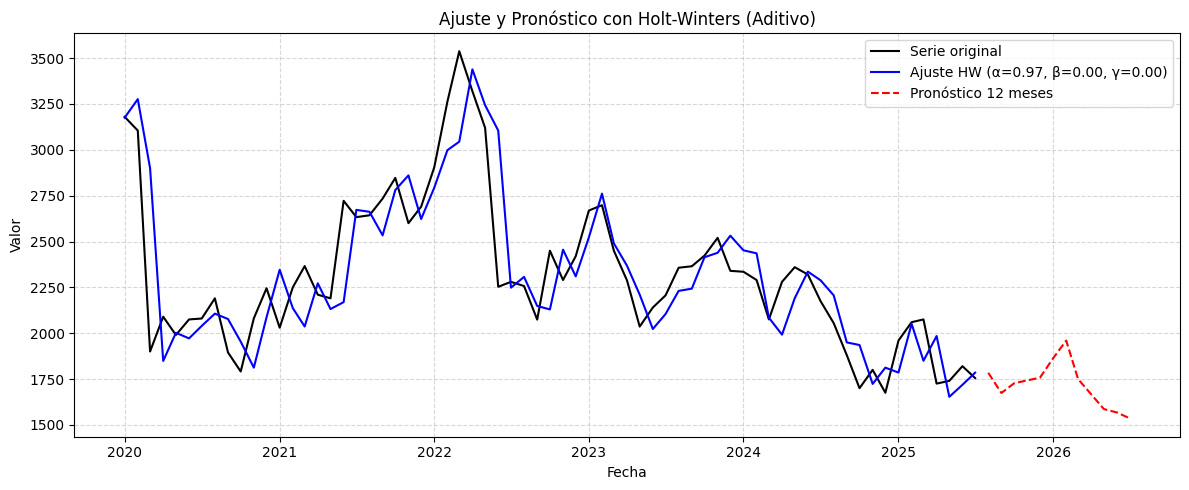
from statsmodels.tsa.holtwinters import ExponentialSmoothing
# Ajustar modelo Holt-Winters aditivo
modelo = ExponentialSmoothing(
serie,
trend='add',
seasonal='add',
seasonal_periods=12
).fit(optimized=True)
# Pronóstico a 12 pasos
pronostico = modelo.forecast(12)
# Extraer parámetros
params = modelo.params
alpha = params['smoothing_level']
beta = params['smoothing_trend']
gamma = params['smoothing_seasonal']
# Graficar serie original, ajuste y pronóstico
plt.figure(figsize=(12, 5))
plt.plot(serie, label='Serie original', color='black')
plt.plot(modelo.fittedvalues, label=f'Ajuste HW (α={alpha:.2f}, β={beta:.2f}, γ={gamma:.2f})', color='blue')
plt.plot(pronostico, label='Pronóstico 12 meses', color='red', linestyle='--')
plt.title('Ajuste y Pronóstico con Holt-Winters (Aditivo)')
plt.xlabel('Fecha')
plt.ylabel('Valor')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.5)
plt.tight_layout()
plt.show()
from statsmodels.tsa.holtwinters import SimpleExpSmoothing, Holt, ExponentialSmoothing
# Ajuste 1: Suavizado Exponencial Simple (SES)
ses_model = SimpleExpSmoothing(serie).fit(optimized=True)
ses_fit = ses_model.fittedvalues
# Ajuste 2: Holt (nivel + tendencia)
holt_model = Holt(serie).fit(optimized=True)
holt_fit = holt_model.fittedvalues
# Ajuste 3: Holt-Winters (nivel + tendencia + estacionalidad)
hw_model = ExponentialSmoothing(serie, trend='add', seasonal='add', seasonal_periods=12).fit(optimized=True)
hw_fit = hw_model.fittedvalues
# Graficar los tres ajustes sobre la serie original
plt.figure(figsize=(14, 6))
plt.plot(serie, label='Serie original', color='black', linewidth=2)
plt.plot(ses_fit, label='SES (nivel)', color='blue', linestyle='--')
plt.plot(holt_fit, label='Holt (nivel + tendencia)', color='green', linestyle='--')
plt.plot(hw_fit, label='Holt-Winters (nivel + tendencia + estacionalidad)', color='red', linestyle='--')
plt.title('Comparación de métodos de suavizado: SES, Holt y Holt-Winters')
plt.xlabel('Fecha')
plt.ylabel('Valor')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.5)
plt.tight_layout()
plt.show()